Contents
立法数の和
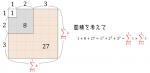
一辺の長さが$1+2+3$の正方形の面積を立法数を用いて求めることができることが上記の内容で理解できるかと思います。
つまり、$1^3+2^3+3^3 = \displaystyle \sum_{ k = 1 }^{ 3 }k \times \displaystyle \sum_{ k = 1 }^{ 3 }k$となります。
$自然数の和 \times 自然数の和$と捉えることができ、
$ \displaystyle \sum_{ k = 1 }^{ n }k^3 = \lbrace \frac{n(n+1)}{2} \rbrace \times \lbrace \frac{n(n+1)}{2} \rbrace$となる。つまり、立法数の和は以下で表現できる。
$$\displaystyle \sum_{ k = 1 }^{ n }k^3 =\lbrace \frac{n(n+1)}{2} \rbrace^2$$







